FIBONACCI

Sebastian Renzo Agustin Rossana

Read more publications on Calaméo

#include<iostream>
	using namespace std;
	int fibo(int n)
	{
	if(n == 0 || n == 1)
	return n;
	else
	return fibo(n - 2) + fibo(n - 1);
	}
	int main()
	{
	cout<<"\n FIBONACCI \n\n";
	int i, num ;
	do
	{
	cout<<"Ingrese un numero entero y positivo: ";
	cin>>num;
	} while(num < 0);
	cout<<"\nLa serie es: \n\n\t";
	for(i=0; i<num; i++)
	{
	if(fibo(i) != 0)
	cout<< ", ";
	cout<< fibo(i);
	}
	return 0;
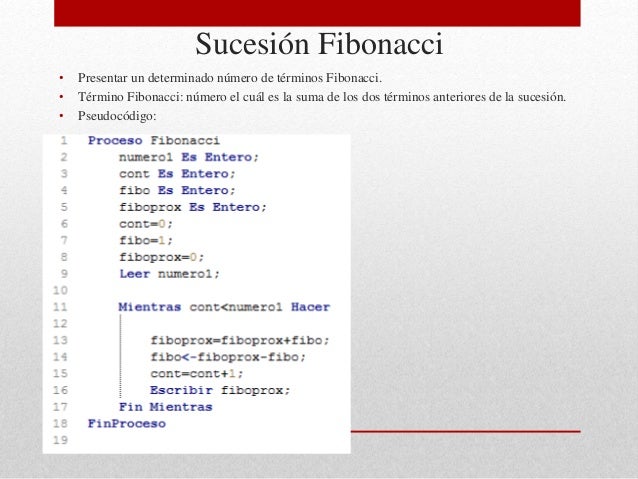
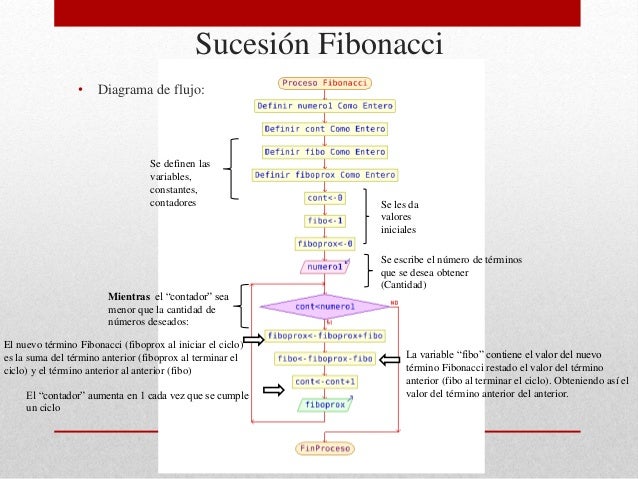
	} Fuentes- http://blog.martincruz.me/2012/09/recursividad-serie-de-fibonacci.html La sucesión de Fibonacci La sucesión de Fibonacci es la sucesión de números: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... Cada número se calcula sumando los dos anteriores a él. El 2 se calcula sumando (1+1) Análogamente, el 3 es sólo (1+2), Y el 5 es (2+3), ¡y sigue! Ejemplo: el siguiente número en la sucesión de arriba sería (21+34) = 55 ¡Así de simple! Aquí tienes una lista más larga: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ... ¿Puedes encontrar los siguientes números? La regla La sucesión de Fibonacci se puede escribir como una "regla" (lee sucesiones y series): la regla es xn = xn-1 + xn-2 donde: xn es el término en posición "n" xn-1 es el término anterior (n-1) xn-2 es el anterior a ese (n-2) Por ejemplo el sexto término se calcularía así: x6 = x6-1 + x6-2 = x5 + x4 = 5 + 3 = 8 Razón de oro Y hay una sorpresa. Si tomas dos números de Fibonacci consecutivos (uno detrás del otro), su cociente está muy cerca de la razón aúrea "φ" que tiene el valor aproximado 1.618034... De hecho, cuanto más grandes los números de Fibonacci, más cerca está la aproximación. Probemos con algunos: A B B / A 2 3 1.5 3 5 1.666666666... 5 8 1.6 8 13 1.625 ... ... ... 144 233 1.618055556... 233 377 1.618025751... ... ... ... Usar la razón de oro para calcular números de Fibonacci Y es más sorprendente todavía esta fórmula para calcular cualquier número de Fibonacci usando la razón de oro: Increíblemente el valor siempre es un número entero, exactamente igual a la suma de los dos términos anteriores. Ejemplo: Fuente- http://www.disfrutalasmatematicas.com/numeros/fibonacci-sucesion.html